제곱합 공식을 눈으로 손으로 만져보면서 감상하고 싶다.

이를 위해서 교구를 만들기 위한 블럭코딩 과정, 프린팅, 공식 이해를 위한 교구 조작의 과정을 소개하겠다.
[1] 코드로 모델링 하기
Tinkercad code block 으로 큐브 피라미드 만들었다.
아래 그림이 결과물이다.

코딩에 templete object 는 두개 사용되었다.
templete 하나.
먼저 사용할 정육면체를 만든다.
cube라고 이름을 부여했다. 한변의 길이는 변수 a를 지정해서 입력하였다.

이제 새로운 개체를 하나 더 생성하고 블럭 코딩을 하였다.

| 1> 피라미드 모양의 각 층은 i 변수로 표현될 것이다. count with 명령어를 사용해서 i 변수가 0 또는 1부터 원하는 6층까지 반복하게 한다. 이때 층의 높이를 바꿀 계획이라면, 변수 'b'를 사용하용하기로 한다. 요약: 구문의 의미는 계단의 층 i 가 1층부터 b층 까지 1단위로 변하면서 어떤 명령을 수행할 것이라는 의미이다. |

| 2> i 변수는 각 층의 정사각형의 한변의 길이와 같다는 것을 기억해야 한다. 그래서, 이것을 정사각형의 가로의 길이로 사용하는 반복 명령을 삽입하였다. 각층마다 해당 층의 횟수만큼 반복하여 어떤 명령을 수행할 것이다. 이 명령은 cube라는 개체를 가져온다음 가로축으로 한칸씩 이동하는 명령이다. (여기서는 -1을 사용했는데, 1을 넣어도 상관없다. ) |

| 3> 한칸씩 이동할 때마다 또 다른 반복 명령이 수행된다. 세로로 i 변수만큼 방금 생성한 개체를 복사해서 세로축으로 한칸 이동시킨다. (여기서는 -1을 입력했는데, 1을 입력해도 상관 없다.) |

| 4> 이렇게 각 층마다 정사각형이 완성되면 모든 개체를 선택한 후 한칸 위로 올린다. |

| 5> 모든 작업이 완성되면, 처음 생성했던 cube는 지워준다. |

| 6> 위의 작업이 가능하려면, 필요한 변수에 대한 값을 설정해야 한다. 확인하자. |
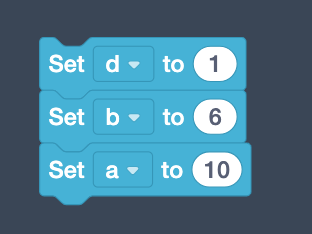
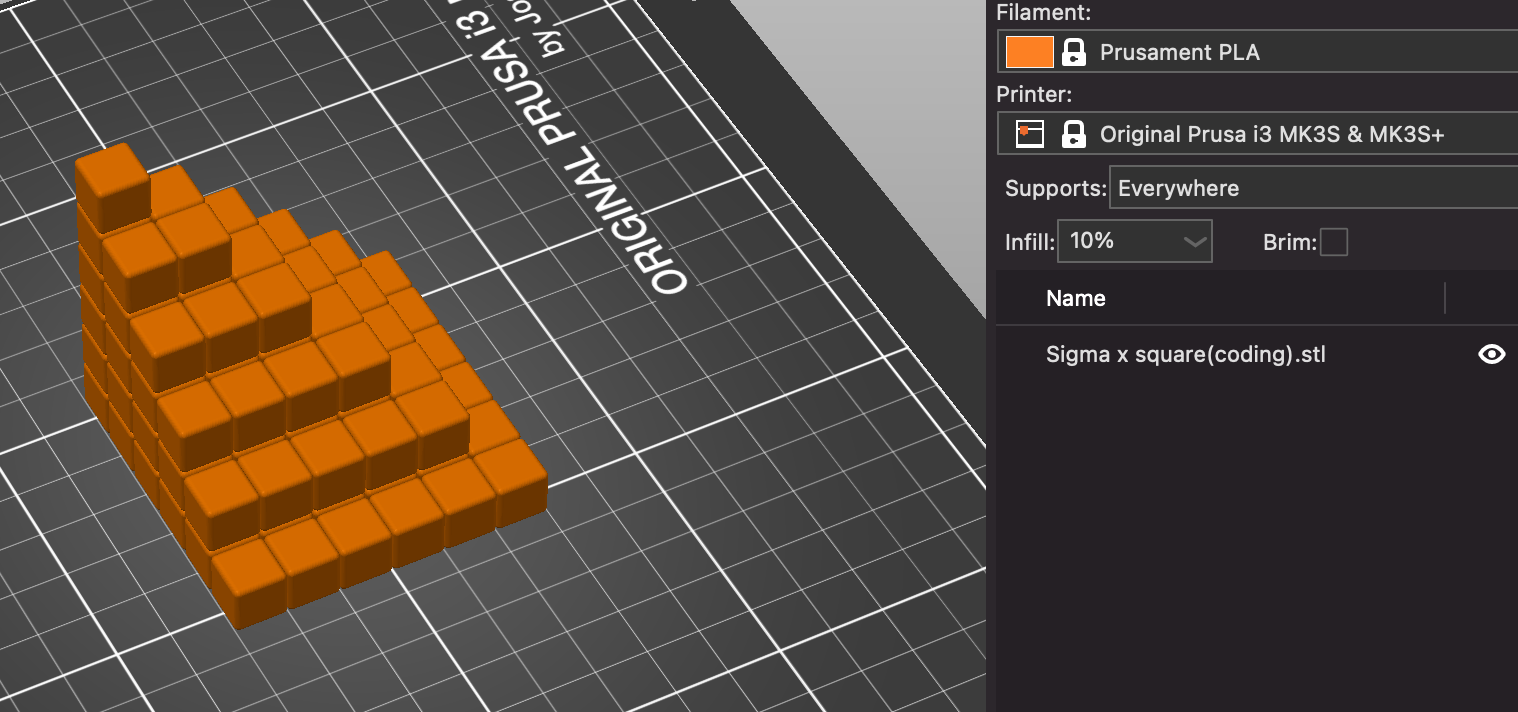
[2] 'stl' export, 슬라이서로 가져오기.
Slicer 로 stl file 가져오기 하고, 슬라이서 설정이나 모델의 크기, 위치 등을 점검 하였다.
오류 메세지가 뜨면, 모델링 과정을 다시 점검해야 한다.
다시 모델링을 해야 할 수도 있다.
[3] Gcode 생성한다.
slicing 해서 Gcode 생성한다.
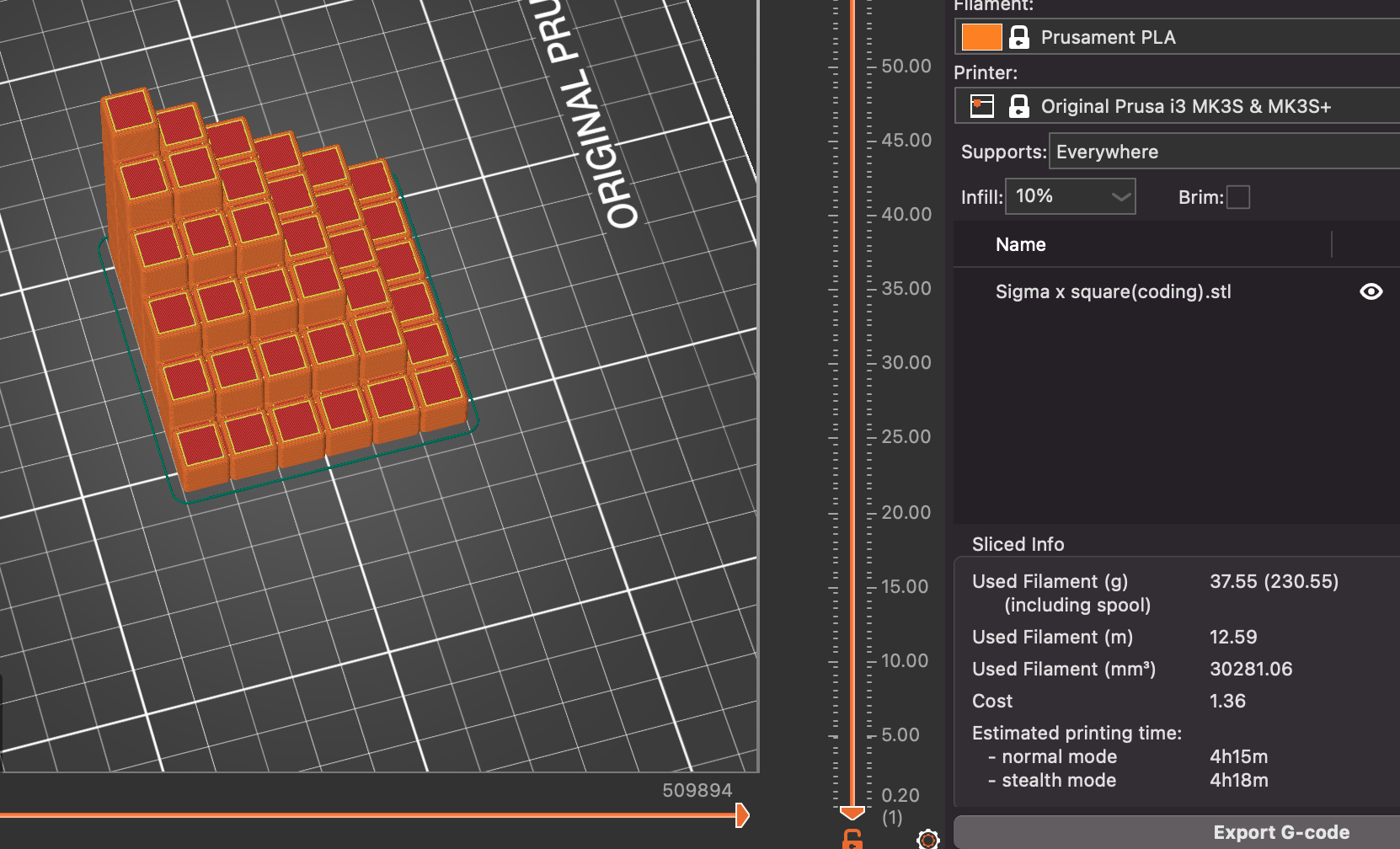
이때 생성된 Gcode에서 써포트의 모양등을 살펴 보고, 뭔가 이상하다 싶으면 다시 모델링 한다.
처음 모델링 한 개체에서 써포트가 많이 생성된 것이 이상했고, 어딘가 빈 공간이 모델 사이에 있을 것만 같은 찝찝함 때문에 다시 모델링하였고, 다시 Gcode 생성하였다. 이제 써포트가 생성 안됐는데, 이 모양이 더 타당해 보여서 이 Gcode를 선택하였다.

[4] 프린트 한다.
그리고 프린트 한다.
6개 할 것이다.

준비됐으.

[5] 제곱합의 공식 이해하기
프린트 한 결과로 제곱의 합 공식 알아보기
1) 정육면체 피라미드의 모양은 제곱의 합을 나타난다.
우리는 6층까지 피라미드를 만들었으므로,
각 층의 큐브들의 개수는 다음과 같이 나열할 수 있다.
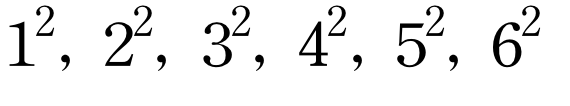
피라미드의 부피는
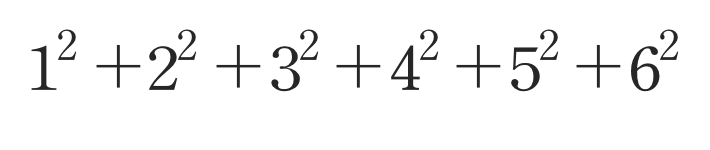
간단한 수식으로는 아래와 같이 표현 할 수 있다.
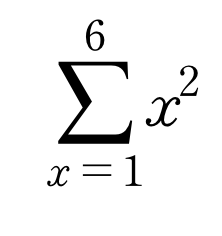
이것은 6층까지 쌓은 큐브 피라미드의 부피를 나타낸다.


이제 일반화해서 생각해 보자.
n 층까지 쌓은 큐브 피라미드의 부피로 일반화 해서 표현하면, 다음과 같다.
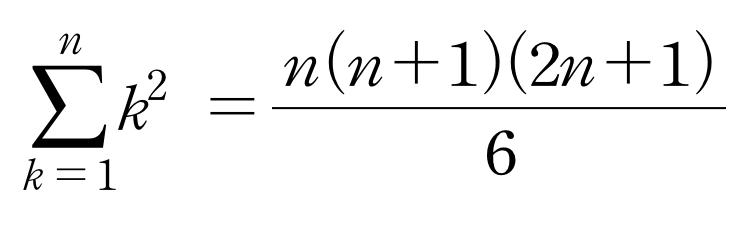
6층짜리 피라미드 6개를 모으면, 아래와 같이
가로, 세로, 높이의 길이가 각각
6, 6+1, 12+1
인 직육면체를 만들 수 있다.
7층짜리 피라미드 6개를 모으면,
7, 7+1, 14+1 을 가로, 세로, 높이로 하는 직육면체를 만들게 되고,
마찬가지로
8층짜리 피라미드 6개를 모으면,
8, 8+1, 16+1을 가로, 세로, 높이로 하는 직육면체를 만들 수 있다.
2) 이제 제곱합의 공식을 알아보자.
피라미드의 층수에 상관없이,
이 직육면체의 부피를 6으로 나누면 한개의 피라미드의 부피가 된다.
일반화해서 생각하면
n층으로 쌓은 피라미드 6개를 모아 만든
직육면체는
가로, 세로, 높이가 각각
n, n+1, 2n+1
이고,
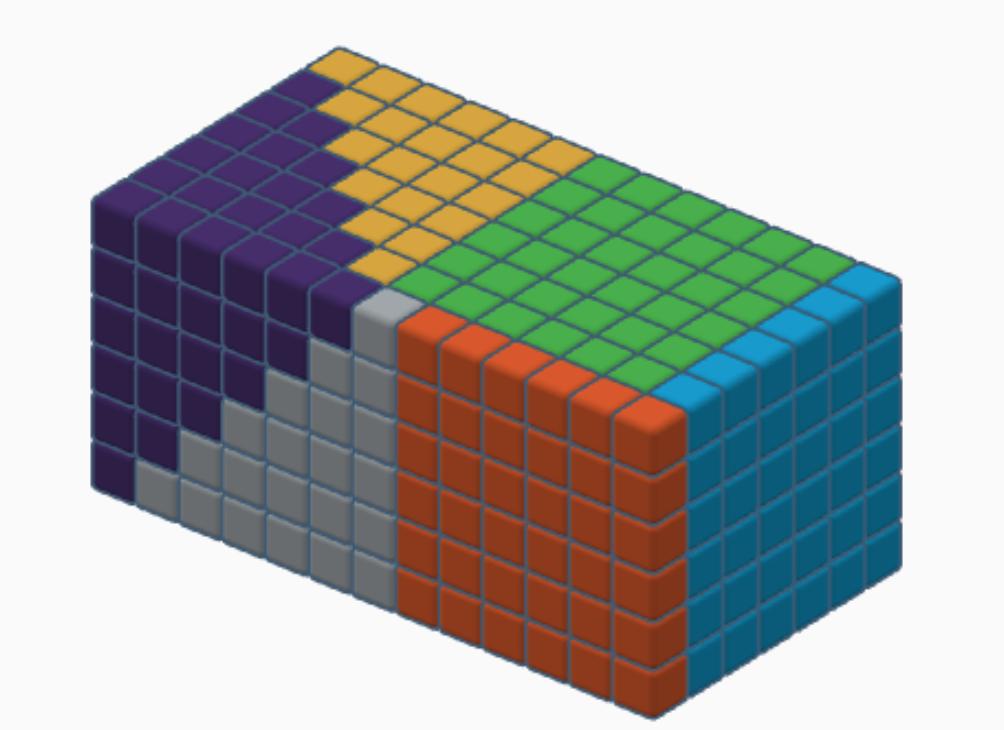
따라서 직육면체의 부피는 n(n+1)(2n+1)이므로
피라미드 한개의 부피는 아래의 식이 되는 것이다.
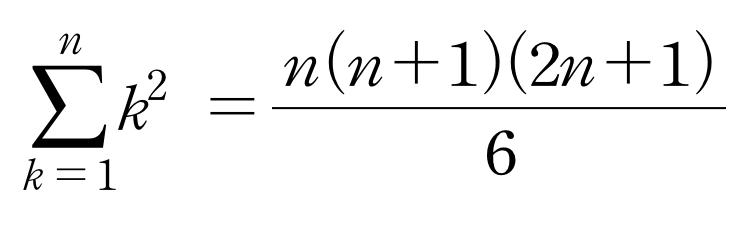
입체들이 만든 모양과 이 입체들의 관계를 잘 생각하면서 제곱합의 공식을 기억하자.

[프린팅 결과 감상]


Volume of a cuboid made with 6 pyramid {with n_th story} is
n(n+1)(2n+1)
hence, a volume of a pyramid is division of the volume of a cuboid.
thus, we get the formula.
'알음다운 > 수악(數樂)' 카테고리의 다른 글
| Sum of N (N=1, 2, 3,...) (0) | 2024.05.23 |
|---|---|
| Sum of n^3 [with 3D printing] (0) | 2024.05.20 |
| Story of a Silla tower(CheomSeongDae) (0) | 2024.05.14 |
| 첨성대(4D frame) (0) | 2024.05.09 |
| 전도테이프 이용한 카드 아트 제작 (0) | 2024.04.24 |