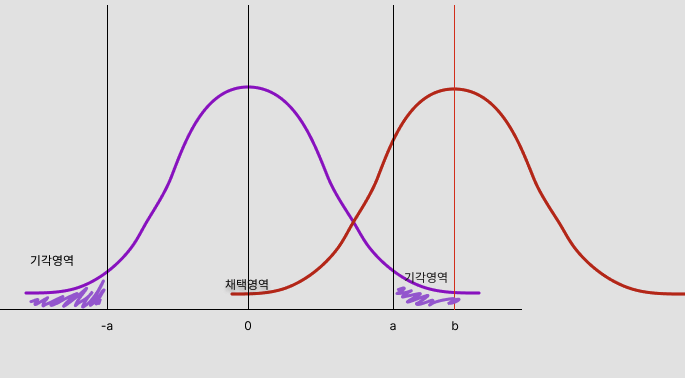
연구 상황을 통해 유의 수준을 이해해 보자. 수학 영재를 판별하는 검사지를 개발하는 연구를 한다 치자. 귀무가설: 검사지가 영재판별에 효과가 없다. 대립가설: 검사지가 영재판별에 효과가 있다. 이렇게 가설을 세우게 되고, 귀무가설이 기각되면, 반증을 통한 증명전략에 의해, 대립 가설을 선택할 수 있다. 여기서는 이해를 위해 증명이란 용어를 사용했지만, 추론 통계에서는 확률을 이용하게되고 엄밀히 증명은 아니기 때문에, 증명이라는 느낌의 통계적 용어, '유의성 검정'이라는 용어를 대신하여 사용한다. 그렇다보니 두가지 오류의 발생 가능성이 생긴다. 1종오류는 귀무가설이 참인데, 기각하는 오류. 2종 오류는 귀무가설이 거짓인데, 채택하는 오류. 1종오류를 범하면 잘못된 검사지가 영재판별에 사용된다. 이 확률를 ..