연구문제가 있었고,
모집단을 대표할 것 같은 표본을 정하고, 자료를 수집했다.
자료를 수집하고 평균을 측정했다고 해서 그 값을 대표값으로 반드시 사용할 수 있는 것은 아니다.
평균이 대푯값으로써 가치가 있는지 판단하기 위해서 표준편차도 살펴보지만,
표준편차 말고도 정규성(Normality)도 검사한다.
통계 분석은 정규성 가정을 하고 진행된다.
즉, 평균값을 대표값으로 사용하겠다는 말의 다른 표현이라고 보면 된다.
표준편차 1, 2, 3에 따라 68%, 95%, 99% 확률로 정규분포를 따를 것으로 가정한다음 분석을 진행한다.
이에따라, 내 표본의 평균이 모집단의 평균을 땡땡 평균에따라 반영한다고 주장 할수 있다.
자 그럼 정규분포란 무엇인가?
아래 그림을 보자.
정규분포는 평균값과 중앙값과 최빈값이 일치하며, 곡선의 모양이 종모양이다. (Bell-shaped distribution)
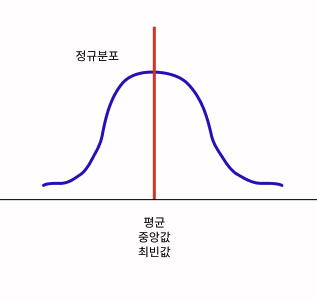
그럼 정규분포가 아닌 비대칭 분포를 알아보자.
한쪽으로 종의 뾰족한 부분이 치우쳐 있으면 비대칭 분포라고 하는데,
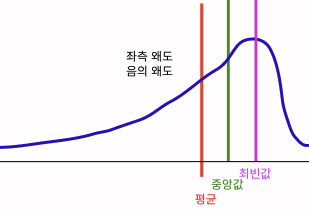
아래 그림처럼 평균이 실제 분포보다 왼쪽에 위치해 있으면 좌측 왜도(좌측 치우침), 혹은 음의 왜도가 있다고 설명한다.
왼쪽으로 꼬리가 길어서 '왼쪽 꼬리 분포'라고 부르기도 한다.
그냥 영어로는 negative skewness.
마찬가지로
아래 그림처럼 평균이 최빈값이나 중앙값보다 오른쪽에 위치해 있다는 것은 오른쪽 꼬리가 길다는 뜻이고, 많은 자료들이 오른쪽에 있다는 뜻이므로 (자료의 값들은 왼쪽이 크지만) 우측 치우침, 우측 왜도, 양의 왜도가 있다고 설명한다. '오른쪽 꼬리 분포'라고도 부른다. (그림은 꼬리가 좀 짧게 그려졌습니다. 꼬리가 길어서 평균값이 최빈값이나 중앙값보다 오른쪽에 위치하게 됨)

자료의 분포가
비대칭이라고 해서 사용하지 않는 것은 아니다. 수치를 참고해서 사용한다. (주로, 피어슨 비대칭 계수를 참고함)
실질 데이터가 완벽한 정규분포를 이루는 경우는 없기 때문이다.
그렇기 때문에 내가 조사한 자료가 정규분포가 아니라고 해서 크게 실망 할 필요는 없다. 흔하니까.

어쨌든
정규성 테스트라는 것은 분포의 치우침 정도를 알아봄으로써 나의 자료가 사용 가능한지 아닌지 살펴보는 과정이다.
'제삼취미 > 통계' 카테고리의 다른 글
| 귀무가설, 대립가설 역할[교육연구] (0) | 2022.11.23 |
|---|---|
| 연구가설 통계처리 전에 확인할 것 (0) | 2022.11.21 |
| 연속 자료 Continuous Data[교육연구] (0) | 2022.11.20 |
| 범주형 자료[교육연구] (0) | 2022.11.20 |
| 다변량 통계란 [교육연구] (0) | 2022.11.20 |