평균은 나의 자료를 요약하는 간단한 통계 모델이다.
변수값들의 총합을 변수의 개수로 나눈것.
(상황1) 온라인 개별학습이 학생들의 수학 성적에 미치는 영향을 알아보기 위하여
학생들의 수학성적의 변화를 1년동안 관찰하고 싶다.
00학급학생들의 성적을 대표하는 값으로 평균을 선택하게 된다.
이때 이 자료를 대표하는 대표값은 평균을 선택함.
(학생들의 점수의 총합) 나누기 (학생수) 는 (평균).
그렇다면 이 평균값은 이 집단의 성적을 잘 대표하는 도구로 사용할 수 있을까?
평균은 이 집단을 대표할까? 항상?
아니.. 꼭 길티는 않아.

극단적으로 세 과목으로 이루어진 두 학생(점수의 집단이라고 봐도 됨)의 성적 평균을 비교해 보자.
은경이의 세과목 점수는 (1,5,9),
수찬이의 세과목 점수는 (4,5,6)이라하자.
두 명의 평균점수는 같다.
그러나
평균이 두 명의 점수를 잘 설명하는 것 같지 않다.
은경이와 수찬이의 평균점수는 같지만,
과목평균과 각 과목 점수간의 차이가 다르다. 분포가 다르다.
이 차이를 계산해서 설명하면 어떨까?...

이것을 '편차'라고 부른다.
(영어로는 Error라고 부름.)
그러나 편차의 합은 항상 0이므로, 이 문제를 해결하기 위해서,
제곱하여 합한 후 루트를 씌운다.
sum of squared Errors(SS) 편차제곱의 합

그럼 일단 편차 합이 0이 되는 일은 방지했다.
그러나 두 집단의 관찰값이 다르면, 데이터가 많은 집단의 편차제곱합이 커질 것이다.
예를들어,
'음악반학생과 수영반 학생의 국어 성적에 차이가 있는가?'가 연구문제일때,
두 집단의 인원수가 다르다면, 20명, 3000명?
많은 인원의 집단의 편차제곱합이 커지게 된다.
그래서 또 나누기가 필요하다.
이때 편차제곱의 합을 데이터 수 (N)로 나눠준 것을 '분산(Variance)' 이라고 부른다.
N으로 나누면 모집단 분산이라고 한다.
(상황2) 땡땡 학교의 음악반 학생과 수영반 학생의 국어 성적에 차이가 있는가? 라는 연구 문제에서는 모든 집단을 관찰할 수 있으므로
N으로 나눌 수 있다.
(상황3) 그런데 이게 더 일반적 문제나 현상에 대한 탐구로 이어진다면,
땡땡 학교가 우리나라 전체 평균 학교임을 설명 한 후, 자료를 분석하게 되는데,
이때는 땡땡 학교는 전체 집단에 대한 현상을 조사하기 위한 표본 중 하나가 된다.
이때는 나누기 N-1을 한다.
요즘은 빅데이터 수집이 가능해서 수도권과 지방 학교 학생의 수학 성적의 비교도 모집단으로 바로 할 수 있게 되었지만,
아직도 대부분은 표본집단의 자료로 부터 모집단을 추정하게 된다.
실질적으로 우리가 만나게 되는 대부분의 통계처리 상황에는 표본 분산만을 알 수 있다.
그렇다면....

왜 표본 분산은 n-1로 나누느냐?
어떤 한 표본의 입장에서 표본 평균들 중에 자신을 빼면 n-1개의 선택지가 있으므로 자유도 n-1가 되기 때문이다. 표본 분산식은 아래와 같다.

그리고 제곱값은 실제 값과 멀리 떨어져 있으므로 다시 실제값에 가까워지게 하기 위해서
제곱근을 취한다.
이게 표준편차. 이다. 표본의 표준편차.
표본의 평균과 분산을
그림으로 이해해보자.
(수학적으로 일치하는 모델은 아니니 참고만 하시오.)
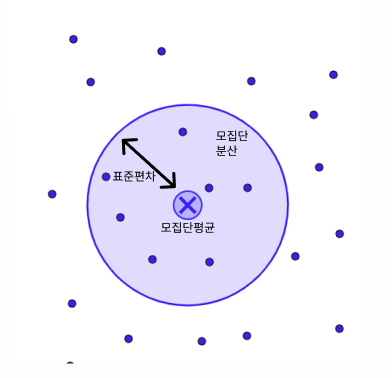
모집단을 점으로 표시하고,
모집단의 평균은 이 점들의 무게중심이라고 생각하자.
그림에서 X 표시한 점을 평균으로 볼 수 있다.
이 점을 중심으로 하는 원을 그리자.
이때, 원의 넓이를 분산으로, 원의 반지름을 표준편차로 생각해보자.
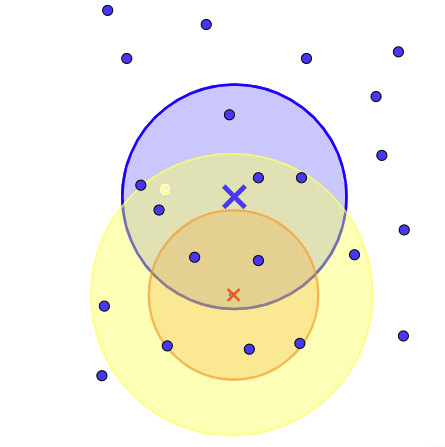
표본을 추출해서 평균과 분산을 구하고 싶다.
노란 범위의 표본을 추출했더니 주황색 점 표본평균과 주황색 원 분산을 얻는다.
이런식으로 생각하면
다양한 표본이 있을거고(빨간색)
이 표본을 통해 모집단의 평균과 분산을 추정할 수 있다.
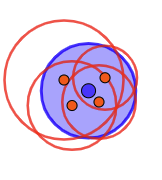
빨간점들의 평균은 빨간점들의 무게중심으로 생각하면 되고, 결국 포본 평균이 모집단 평균에 상당히 쉽게 가까워 질 것이다.

그러나...
표본 분산은 모분산에 그렇게 예쁘게 가까워 지지 않을것 같다.

표본 분산식에는 평균 빼기제곱이 표현되어 있다.
이것을 제곱의 빼기로 생각하자.
오차가 더 커지는 것을 선택했으니 괜찮을것 같다.
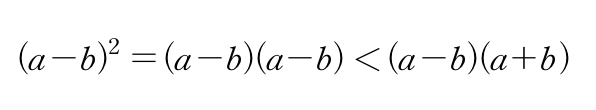
그럼 다시 그림으로 넘어가서
제곱의 빼기는 넓이의 빼기로 이해가 가능하다.
자. 그럼 위 식은
빨간 원에서 파란원을 계속 빼는 것으로 이해할 수 있는데, 이렇게 계속 빼면
결과적으로 파란 부분은 텅 빌 것이다.
그럼 애초에 표본이 n개가 아니고 n-1개가 있었다고 생각해도 되겠지.
그래서 n-1로 나눈다.
(상황1)온라인 개별지도가 수학학습에 미치는 영향을 알아보기 위해
표본 집단의 자료를 수집하게 되고
이 표본의 평균 구하고, 분산과 표준편차도 구한다.
평균은 나누기 n, 분산이랑 표준편차는 나누기 n-1 잊지말것.
표본이니까.
(모집단 아니니까...)
그럼 이제 이 결과의 해석은...
표본의 평균이니까 모평균에서 오차가 있을거라고 가정하여 해석하는데,
표본의 표준 편차가 +- 1이면 68퍼센트, +-2 이면 95퍼센트의 자료가 정규분포에 포함된다고 본다.
즉, 표본이 모집단을 대표하는 정도를 표준 편차로 나타내게 된다.
표본의 평균 사용시 표준편차가 같이 언급되어야 일정 오차범위 내에서 모집단을 대표할 수 있게 된다.
'제삼취미 > 통계' 카테고리의 다른 글
| 일변수 기술 [통계] (0) | 2022.11.20 |
|---|---|
| 통계놀이용 자료는 Gapminder tools에서 (0) | 2022.11.19 |
| 기술통계(descriptive statistics) (0) | 2022.11.18 |
| 통계적 모델이란? [교육연구] (0) | 2022.11.18 |
| 연속자료 범주형자료[통계] (0) | 2022.11.17 |