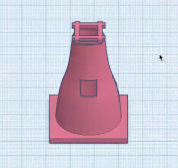
지오지브라로 첨성대의 몸체를 완성했다면 나머지 부분은 팅커캐드를 이용해서 디자인해주자. 첨성대의 몸통이 27개의 단이라는 것도 중요하지만, 몸통에 정사각형 모양의 출입구, 상부까지 사다리를 두고 올라갈 수 있도록 원통 내부에 걸쳐 있는 장대석, 상부에 하늘과 세상을 연결하는 의미의 우물정자, 그리고 33단의 숫자를 완성하기 위해 놓은 다른 단층도 중요하므로 이 부분들을 살려서 첨성대를 완성해보자. (1) 첨성대의 몸통에 정사각형 모양으로 뚫린 출입구와 (2) 첨성대를 받치고 있는 기단, 사각기둥 (3) 첨성대 상단에 우물정자를 이루는 단 (4) 사다리를 걸치고 상단까지 올라갈수 있도록 출입구 윗부분에 원통을 통과하도록 배치한 장대석 4개 를 팅커캐드로 추가해서 그려 넣을 것이다. (5) 다음은 지오지브라..